「統計学 (サイエンス・パレット)」読んだ。
単なる読書メモ。
購入のきっかけは、訳者が上田さんだからというわりとしょうもない理由。
想定読者は統計初学者/やりなおしのあたりと推定。
内容を三行でまとめると、
- 統計の考えの部分に重点を置いて
- その都度分かりやすい例を挙げながら一切の数式を用いず
- 統計の基礎的諸概念と動機について解説してる
良いと思ったところ
本当に基礎の基礎だけど、諸概念の説明と例示がされていて、何もかもが分かりやすい。
訳文も大変読みやすく、あわててその辺の素人を捕まえて無理矢理訳させたようなものが散見される昨今、珍しいくらい良心的だと思った。
また、ベイズ的な考え方についてもきちんと押さえていて、紹介のタイミングもよく(例えば点推定の説明の際に)動機に納得がいきやすい。
後半ではGLMやHMM、ブートストラップやMCMCのような比較的高度(?)な道具立てについてもごく触り程度だが紹介されている。
これは、読者が各人の興味や必要に応じて、それらのキーワードを元に次のステップへ進みやすいようにとの配慮だろう。
大変良い本。これから統計を道具として使う為に学ぶというなら、このような考え方と動機に重点を置いた本を先に読むか、併読した方が有益な結果が得らるように思った。
少し気になったところ
数式にアレルギーが無い人にとっては、数式無しは逆に辛かろうと思う。
文字いっぱいで少しのことを言うのに結構言葉を尽くしているのだけれど裏目に出る層はいると思う。
多分そういう人は想定読者じゃないので、読んでも仕方が無いかもしれない。
また、後半の高度な道具立てのあたりはキーワードの羅列気味になっていて少し押し込め過ぎかなぁとも思った。
総括
とても良い本と感じた。このように動機と考え方に根ざした書籍だと、
最近読んだ「エンジニアの為のデータ可視化[実践]入門」もその類いかと思う。そちらも良い本。
ただし、(Ω, F, P)の三つ組みと日夜戦ってらっしゃる方々とってはあまり意味が無いですよ、と。
類書の煽り文句に負けず、マジョリティを獲得して欲しいなと思いましたとさ。
切符の番号とかナンバープレートの4つの数字と+−×÷を使って10を作るアレを解いてみる
切符にプリントされている4個の数字とか、ナンバープレートに書かれている4桁の数字を、四則演算のみを使って10にするという遊びあるじゃないですか。
そう、あれ。あれです。誰か名前を付けていてもよさそうなんだけど、特別名前が付いている訳でもなさそうなあれ。
どうも海外では、これと似たようなゲームを出題するTV番組があったらしく、そこからCountdown numbers gameという名前で呼ばれているらしいです。
ルールはもうちょっと複雑で、数字が6個だったり、10にするんじゃなくて、その都度違ったり、時間制限があるとか。
これを計算機で解く場合、おそらく一番単純な方法は、葉ノードが数字、接点が演算子の木を全通り出力 → 評価という流れかと。
そういうわけで、実装してみた。例によってJavaScriptです。
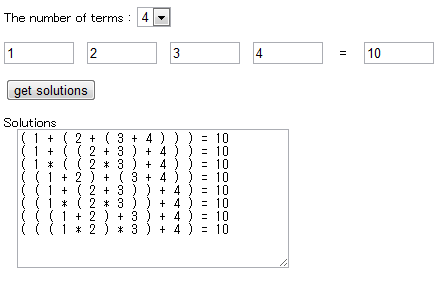
遊び方は見たまんま。
計算したい条件(ナンバープレートの数字と、作りたい10という数字)を入力すると、可能な計算式が全て出ます。4つの数字以上にも対応、途中計算で分数が出てくるものも解として出力します。
大昔に、auの携帯向けのフリーアプリで、まさにこの問題をプレイヤーに解かせるというゲームがあったのですが、困ったことに、自力で解けないときに回答が出てこない(すごいストレス)&なんか解けそうに無い問題が出てくる(理不尽)という代物で、非常に不満だったのですが、これがあれば万事解決。
これを使えば暇なドライブでどうしても解けないナンバープレートを見つけたときに、「解なし」と自信たっぷりにいえる、その快感に酔いしれること請け合いです。
GWの単調なドライブのお供に是非。
追記
10 puzzle とか Make 10とかいうらしい。解く前にググれ、か。
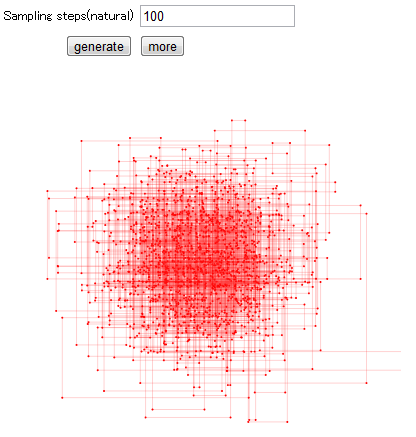
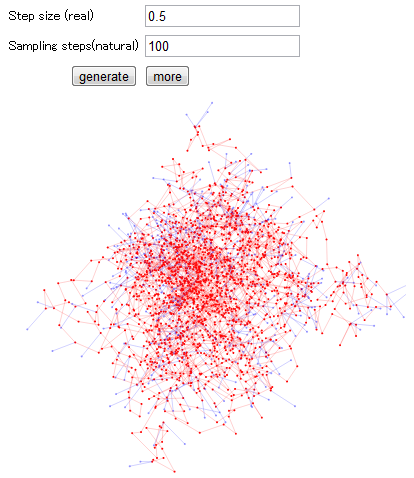
モンテカルロ法とJavaScriptでπ
これはもう説明が全く不要な、コード書く人なら間違いなく通る、モンテカルロシミュレーションでπの値を計算しようという遊び。
これはとても楽しい。視覚化されると楽しさ10倍。というわけでわりと投げやりにJavaScriptで書いた。
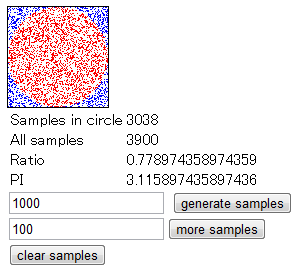
ここであそべる
画像にあるサンプル点は全て1個1個がdivなので、1万サンプルとかやると真面目に死にますので気をつけて。
あと、計算誤差については何も考慮せず作ったので、ある程度の精度以上は出ません。というか、非常に精度が悪い。
電車内で暇に任せてiPod Touchで書いたコードに枝葉を死ぬほどつけたらなんかできたのでとりあえず公開。
括弧対応をとる
一瞬必要だったので。corr_tableをいじればどんな組でも可。括弧の交差はダメ。
var corr_table = { '(' : ')', '[' : ']' }; function checkBrackets( t ){ var stack = []; for( var i = 0; i < t.length; ++i ){ for( var j in corr_table ){ if( t[i] == j ){ stack.push( j ); break; } else if( t[i] == corr_table[j] ){ if( stack.pop() != j ){ return false; } else { break; } } } } return stack.length == 0; }
ん?はてダってカテゴリつけないとだめなん・・・?
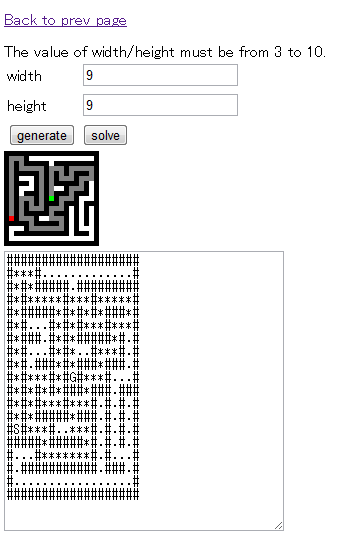
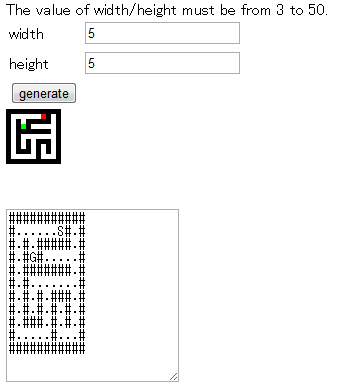
迷路生成器と迷路解き器
解き器って。
折角迷路生成器を作ったなら、ソルバ(逃げた)も書いたほうが楽しい。というわけで作った。
生成はみんな大好き深さ優先、ソルバは普段あまりお目にかかりにくい幅優先。学生のお勉強にはもってこいですね。社会人のやることではない。ない。
加えて、生成器は生成の様子が分かるようにぐりぐり動くように改造されてしまった。
ここまでやったら次はA*か。
コードはびっくりするほど汚い!
どうもhatenaではiframeを日記に突っ込む方法があるらしいのでそれを貼り付けられれば一番いいのだけど、これに限って言えば描画をサボっていてかなり重いのでどの道無理。
題名なし
よくあるnext_permutationのサンプル
#include<iostream> #include<vector> #include<algorithm> void printvec( std::vector<int> &v){ for( int i = 0; i < v.size(); ++i ){ std::cout << v[i] << " "; } std::cout << std::endl; } int main(){ std::vector<int> v, e; v.push_back(1); v.push_back(2); v.push_back(3); printvec( v ); while( std::next_permutation( v.begin(), v.end() ) ) printvec( v ); return 0;
出力
1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1
ループを変えてみる
for( int i= 0; i < 12; ++i ){ std::cout << std::next_permutation( v.begin(), v.end() ) << " "; printvec( v ); }
出力
1 2 3 1 1 3 2 1 2 1 3 1 2 3 1 1 3 1 2 1 3 2 1 0 1 2 3 1 1 3 2 1 2 1 3 1 2 3 1 1 3 1 2 1 3 2 1 0 1 2 3
おお、覚えていらっしゃるのか。